Reading Levels with Textstat

Reading Levels with Textstat

There are lot of things you can do with textual data. You can do topic modeling, PoS tagging, sentiment analysis, stylometry, and term frequency. Something else you can do is reading level analysis. Now, most of the time, this might not have too much utility. However, you might find it a useful feature in feature engineering.

One of the nice Python libraries I found for calculating reading levels is Textstat. There are a number of different tutorials on this topic and to be honest, I can’t say that they are insufficient. Indeed, the documentation for Textstat answers most questions you could have in terms of use. However, I thought it would be nice for me to write up my own little guide to the subject because I’ve noticed a few things.

Throughout this, I’m using 10 ebooks I downloaded from the Guttenberg Project. I chose the 10 most popular books over the last 30 days. I had to do this manually because they strongly discourage using robots (they will ban your IP address).

I started by combining those text files and doing a bit of light cleaning of them. That code is in a separate ipynb that I’ve uploaded and I’ve linked to here. I’ve included everything we’re doing here in another ipynb located here. I also have everything from the resulting NDJSON to the original books from Project Gutenberg included here.

We start by reading in the data after importing our libraries.

import pandas as pd
import textstat as ts

books = pd.read_json("top-10-projbg-books.ndjson", lines=True)

Our first thing we’re going to check is the Flesch Reading Ease Score and Flesch Kincaid Grade Level (based off the Flesch Reading Ease). You can read more about them on Wikipedia, but they were originally meant to provide a way for evaluating textbooks.

%%time
books["fl_ease"] = books["text"].apply(ts.flesch_reading_ease)

%%time
books["fl_kn_grd"] = books["text"].apply(ts.flesch_kincaid_grade)

Our next two measures work differently and have different assumptions. They try to represent the years of education it would take to read a work. The Gunning fog index and the SMOG grade . These are both actually better measures than Flesch based scores when it comes to some cases. Generally, they perform better with healthcare texts. Though, I suspect a good bit of that is because they consistently return higher levels in my experience.

%%time
books["gunning"] = books["text"].apply(ts.gunning_fog)

%%time
books["smog"] = books["text"].apply(ts.smog_index)

Our next two measures are different still. Automated Readability Index is computed on a per-character basis while the Dale-Chall involves a list of “easy” words. Both result in an approximate grade level of a text.

%%time
books["ari"] = books["text"].apply(ts.automated_readability_index)

%%time
books["dale_chall"] = books["text"].apply(ts.dale_chall_readability_score)

The final readability measure is an ensemble measure that is unique to Textstat. I think it can be useful on occasion, though it is considerably slower than the other options (since it runs all of them).

%%time
books["ensemble"] = books["text"].apply(ts.text_standard, float_output=True)

Other Metrics

There are two other metrics that Textstat has set up. One of those is the McAlpine EFLAW score that is meant to measure readability for a person who isn’t a native English speaker. The other is a reading speed calculated on a per character basis. Now I have concerns about the validity of the reading speed and think it’s too optimistic. Furthermore, it’s difficult to determine what the per-character speed should be. For myself, I relied on Trauzettel-Klosinski et al, 2012 and went with 16.45 ms per character. In this case, the documentation isn’t clear, but the end result is in seconds to read the work. I had to read through the repo to figure that part out.

%%time
books["eflaw"] = books["text"].apply(ts.mcalpine_eflaw)

%%time
books["reading_time"] = books["text"].apply(ts.reading_time, ms_per_char=16.45)
# mean time per character per Trauzettel-Klosinski et al, 2012

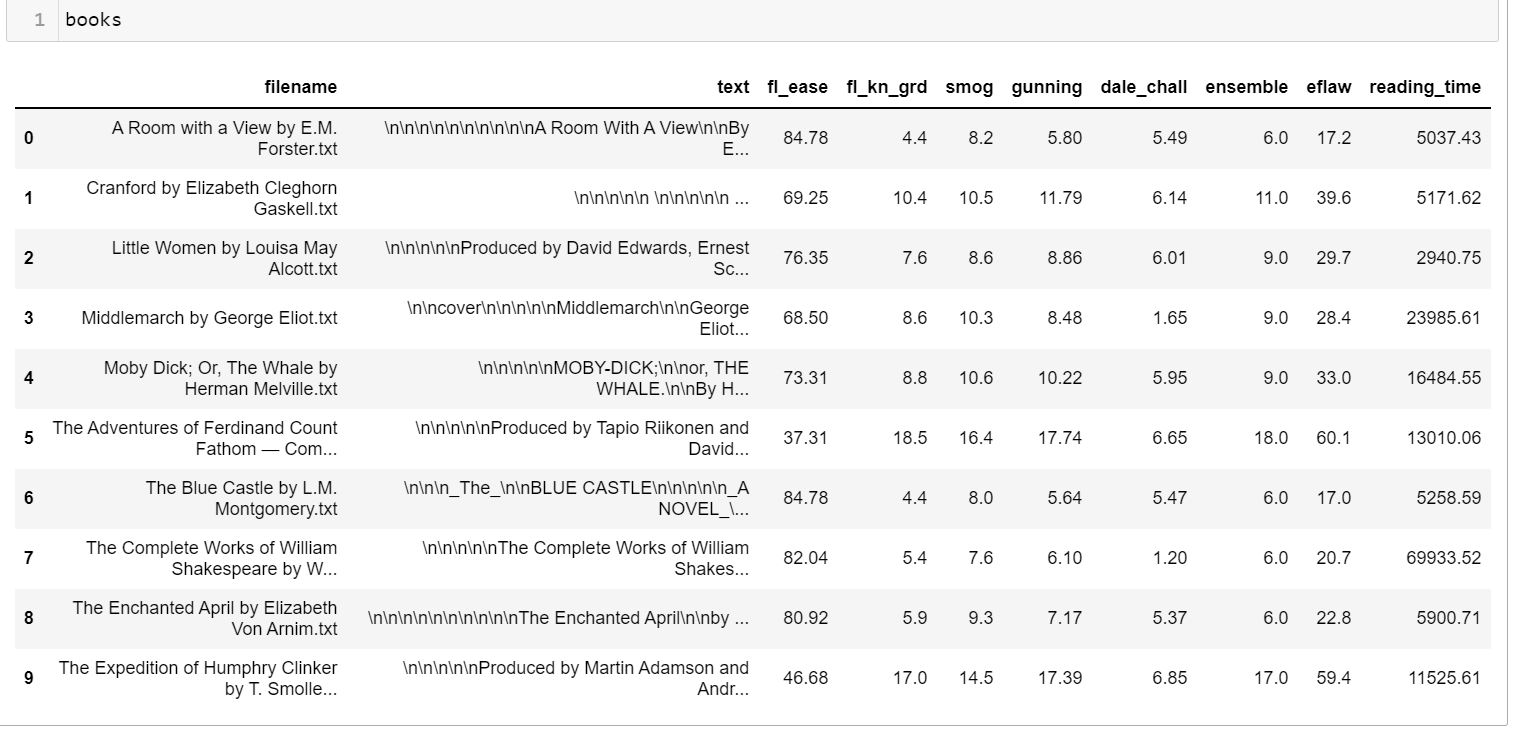
As we can see from the end result of our work here, I have some thoughts. I’m not sure about how well these are performing here. I don’t know if Shakespeare is actually at the 6th grade level in general. I’m especially unsure about the Dale-Chall score of 1.2 which would indicate an average 4th grader can easily understand it. Of course, these shouldn’t be relied on as a gold standard but rather a hint of a direction that things might be.

Different formulas lead to different results unsurprising to think about. Thus, in this case, the text standard is probably our best bet. This is because it is rooted in finding the consensus of the scores. Of course, “best” is probably a bit ambiguous in a lot of respects. For one thing, the metric needs to be one that is understood and accepted. For another, it needs to be one that is considered reliable. It’s important to understand the context which exists for each of these metrics.

The usual Flesch-Kincaid formula can overestimate readability in certain contexts. The SMOG index is better used for technical documents in a lot of respects and is popular in assessing the readability of health documents. However, syllable based readability tests have their own issues, short words may confuse people if they are rare. Other approaches can be found in the Dale-Chall formula that has a list of words that 4th grade students can understand and anything off the list is considered difficult. In general though, any metric here is probably a “good enough” metric in general. Specific use cases require specific testing to ensure reliability and validity of a measure.